Recently, a team of international researchers led by SPST Professor Chen Yulin made a breakthrough in the search for new topological quantum materials and discovered a magnetic Weyl semimetal phase in a ferromagnetic compound Co3Sn2S2. Their work titled “Magnetic Weyl semimetal phase in a Kagomé crystal” was published online in Science on Friday, Sept 20.
The past decade has been witness to exciting progress in the field of topological quantum materials, in that relativistic phenomena can be achieved in easily available table top materials, and the principles of topology can be used for the discovery of materials with exotic physical properties. A recent example of such materials is the Weyl semimetal (WSM), which hosts emergent pairs of linearly dispersing bulk Weyl fermions and unique surface Fermi-arcs (SFAs) that connect the Weyl points of opposite chirality. The unusual electronic structures of WSMs can give rise to many unusual physical phenomena (as will be discussed below), and even inspire theoretical progress as well as new spintronic applications.
In solids, WSMs can exist in crystals that break the time reversal symmetry (TRS) or inversion symmetry (IS). Compared to the IS-breaking WSMs discovered in 2015, the TRS-breaking WSMs provide a playground for the interplay between magnetism, electron correlation and topological electronic structures, which can give rise to rich exotic quantum states (Fig. 1A) ranging from quantum anomalous Hall effect to Axion insulators. Furthermore, TRS-breaking WSMs have other preferred properties. For example, chiral anomaly is easier to observe in materials that have exactly two Weyl points, which is possible only in TRS-breaking WSMs; by preserving the IS, the energies of a pair of Weyl points in a TRS-breaking WSM are required to be the same, making it possible to realize the true nodal WSM phase when the Fermi energy coincides with the Weyl nodes; and finally, the TRS-breaking WSMs are attractive for spintronics applications, as the enhanced Berry curvature, together with its intrinsic magnetism, may lead to unusually large anomalous Hall conductivity and the anomalous Hall angle.
However, despite the many proposed candidates starting from 2011, unambiguous experimental confirmation of TRS-breaking WSM remains challenging. Recently, thanks to an international collaboration between ShanghaiTech University, Max-Planck Institutes and Oxford University, the TRS-breaking, or magnetic WSM were finally discovered in a Kagomé crystal Co3Sn2S2. The international team used angle-resolved photoemission spectroscopy (ARPES) to systematically study the electronic structures of single-crystal Co3Sn2S2, and successfully observed both characteristic electronic signatures of a WSM: the bulk Weyl fermions and the SFAs in its ferromagnetic phase. This finding, further supported by the excellent agreement with ab initio calculations, unambiguously confirms the TRS-breaking WSM phase in Co3Sn2S2, which not only helps explains its exotic physical properties, but also provides a new platform for potential applications.
More details of the work and full text of the work can be found online : https://science.sciencemag.org/content/365/6459/1282.full
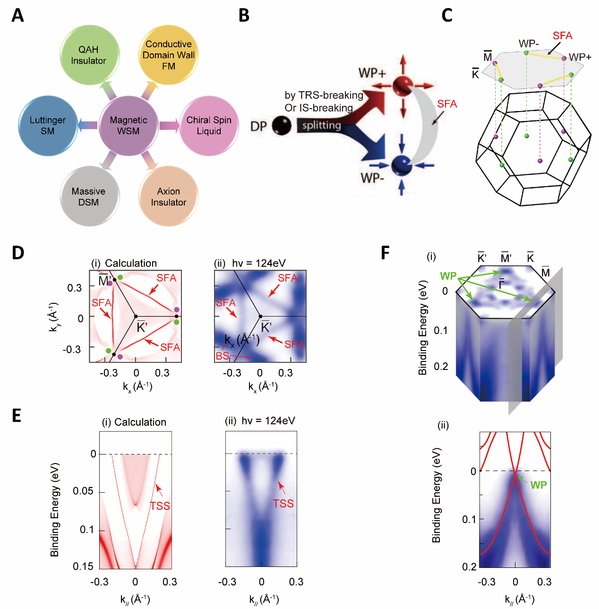
Figure 1 Discovery of magnetic WSM in Co3Sn2S2. (A) Exotic neighboring states of the magnetic WSM can be achieved by tuning parameters such as magnetism, thickness, and electron correlation. (B) A Dirac fermion (DP) can be split into a pair of Weyl points with opposite chirality (marked as WP+ and WP-) by breaking TRS or IS. The two Weyl points are connected by the SFA formed by the topological surface states (TSSs). (C) Schematic of distribution and configuration of the Weyl points and SFAs. (D) Comparison of (i) the calculated Fermi surface (FS) from both bulk and surface states and (ii) the experimental FS. (E) Comparison of the dispersions from (i) calculated TSS and (ii) the experimental TSS. (F) (i) 3D ARPES spectra intensity plot with Weyl points (marked by green arrows). (ii) The measured band shows a linear dispersion across the Weyl point, agreeing well with the calculations (red curves overlaid).


