近日,上科大物质学院光子科学与凝聚态物理研究部潘义明教授 LiFE(光和自由电子)课题组提出一种基于几何位相(geometrical phase)构造的Berry-Maxwell方程,该理论结果发表在国际学术期刊Physical Review B。这一突破性研究将Berry曲率扩展至四维能量-动量空间,并结合了洛伦兹不变性与外尔单极子(Weyl monopole)的高斯定律,为量子力学,电磁学和拓扑物理等领域开辟了全新的研究方向。
研究人员首先通过将Berry连接和Berry曲率从三维动量空间扩展至四维能量-动量空间,构建了一个Berry四维连接。这个扩展过程引入了一个电场形式的Berry曲率,称为“互易电场”(reciprocal electric field)。在此基础上,研究团队利用波恩互易性(Born reciprocity)【图一所示】,将Berry四维连接与传统电磁学中的四维电势联系起来,构建出了描述互易电磁场动态的Berry-Maxwell方程。
为了确保这些方程的普适性,研究人员引入了洛伦兹不变性作为约束条件,适用于四维能量-动量空间。此外,他们还结合了外尔单极子的高斯定律,将其作为Berry-Maxwell方程的基础【图二所示】。这一构造过程不仅揭示了Berry-Maxwell方程的自对偶和对偶结构,还确保了它们与传统Maxwell方程之间的密切联系,但又在物理现实中保持独立存在。
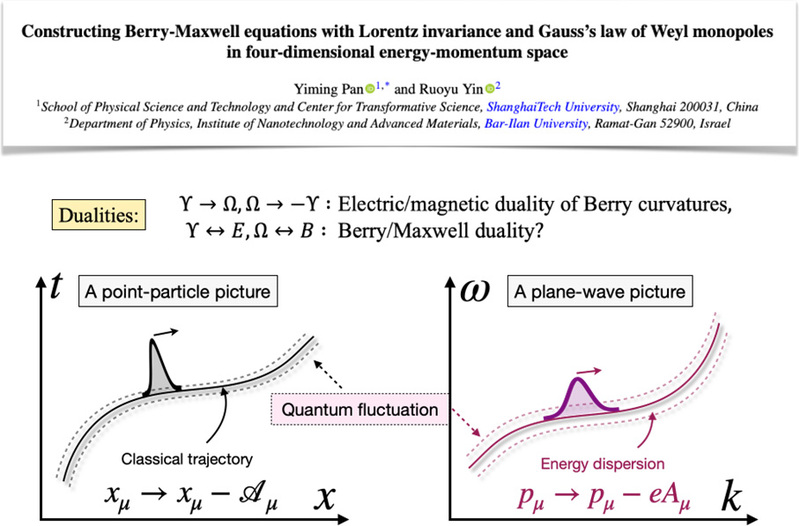
图1:Maxwell方程的电磁对偶以及Berry-Maxwell方程的Berry 曲率对偶。

图2:本文中构造的Berry-Maxwell方程跟通常的描述电磁场的Maxwell方程在无源无流情况下的相似性。我们依然存在一个问题,即Berry-Maxwell方程是否描述真实的物理现象?有待进一步研究。
研究团队进一步探讨了三种可以验证这一理论的实验效应:首先,通过洛伦兹变换对外尔单极子的运动进行观察,预计能够引发电场形式的Berry曲率【图三所示】;其次,团队预测了互易Thouless泵浦现象,这是Berry-Maxwell方程在能量-动量空间中的拓扑效应之一;最后,研究人员推导出了Berry-Maxwell方程的平面波解,即使在没有外尔单极子或电流的情况下,这些波解依然存在,并可能在实验中表现出类似于时空中的点状事件。
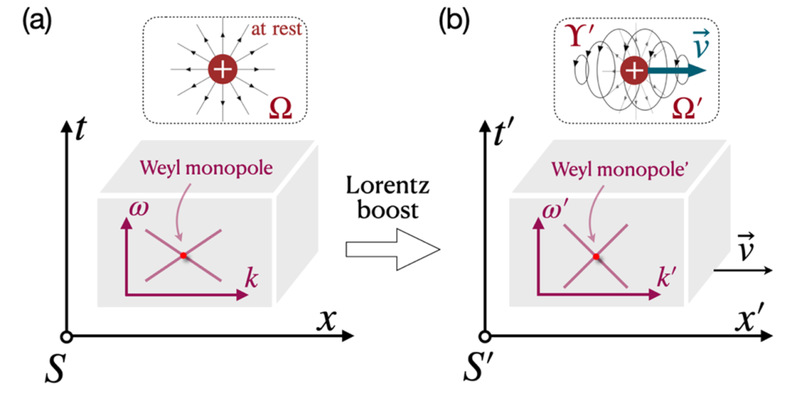
图三:我们提出一种Lorentz boost of Weyl monople的实验方案,可产生非平庸的电场型Berry曲率(),用于实验检验Berry-Maxwell方程的存在性和正确性。


